Simultaneous Equations x+y=4 and x^2+y^2=40

This question consists of a linear equation and a quadratic equation, which you have to solve using the simultaneous method. There will be two sets of solutions for both x and y, because if you were draw the graphs of both equations, the straight-line graph will intersect the quadratic curve in two places giving two solutions.

The linear equation x + y = 4, rearranges easily to make an expression for y, which substitutes into the quadratic equation x² + y² = 40.

Substitute the expression for y into x² + y² = 40 to give a quadratic equation. As you can see, you multiply out the brackets and add up the like terms to make a quadratic. This is simple and straightforward.

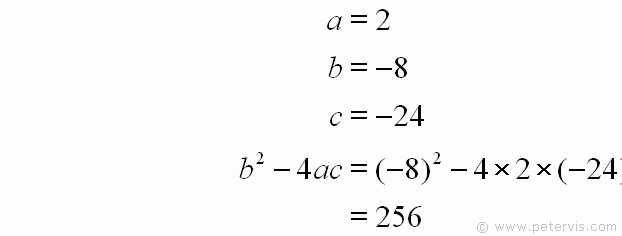
The coefficients of the quadratic are a=2, b=-8, c=-24. Just plug these into the standard quadratic equation formula to calculate the two root solutions. The first step is to calculate the discriminant, which is the b² - 4ac part under the square root sign. As you can see, this is a positive number of 256, which means that the roots will be real.

Now substitute the rest of the numbers into the quadratic equation formula to give two real roots of 6, and -2.

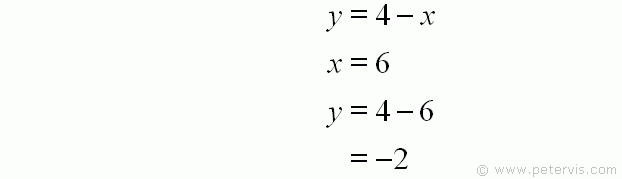
Now that we have values for x we can find the values for y by substituting them back into the expression y = 4 - x. Therefore, when x=6, y=-2.

Finally, substituting again for the other root, when x=-2, y=6.