Integrate 1/cosx

To integrate 1/cosx, also written as ∫ 1/cosx dx, 1 divided by cosx, (cosx)^-1, we start by using standard trig identities to to change the form.

We recall the standard trig identity for secx.

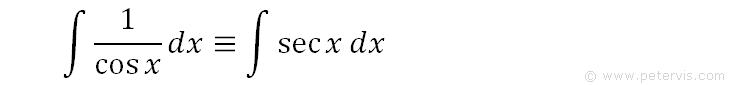
Therefore the integral of secx is the same thing, or identical in other words. At this point, we can simply look up the integral of secx in our formula booklets as there is a standard solution for this, and call it a day. However, we want to show some form of derrivation at least.

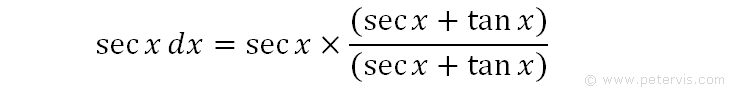
If we were to multiply and divide by secx + tanx, then we have not changed anything, but it gives us something to play with.

As you can see, this part equals 1, hence mathematically, it has not changed anything.

Hence, our integration problem can be rewritten as shown above.

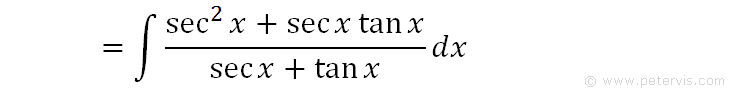
We multiply the numerator by secx to give the expression above. As you can see, now the numerator is the differential of the denominator, which is what we were aiming for so that we could use the u substitution. It will all become clear in the following lines.

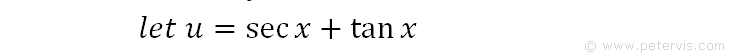
We let u = secx + tanx. Or in other words u is the expression in the denominator.

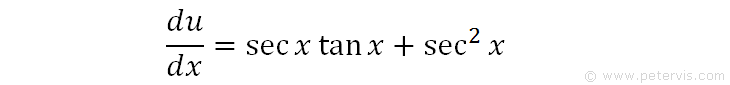
Then du/dx is the expression shown above. As you can see, it is the same as what we have in the numerator of our integration problem.

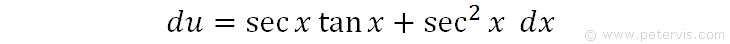
We rearrange it for du by moving dx to the RHS.

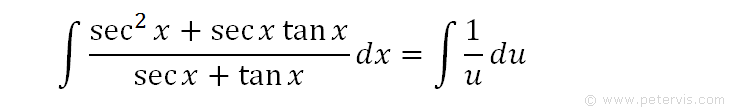
We now replace the numerator with du, and denominator with u using substitution. Hence we get a new and simpler integration problem in terms of u and du.

The integral of 1/u is a standard solution in formula books, which we can look up. We also replace u with secx + tanx.

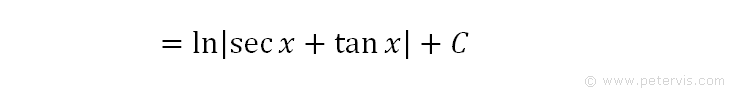
Therefore, this is the final solution, where C is the integration constant.