Integrate 2sec^2x tanx

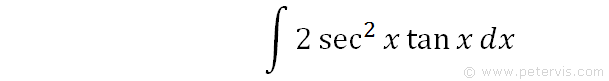
To integrate 2sec^2x tanx, also written as ∫2sec²x tanx dx, 2 sec squared x tan x, and 2(sec x)^2 tanx, we start by recognising that the differential of one half is within the other half of the same expression. In this case, the differential of tanx is sec squared x, which should fill you with great confidence to use the u substitution method.

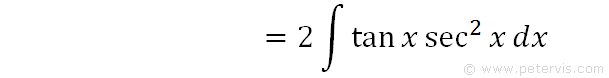
We can move the constant 2 behind the integral, and rearrange the terms so that the substitution will be easier to see. Our goal is to substitute sec squared x dx with du, and the following steps show how to do that.

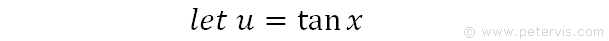
Let u = tanx.

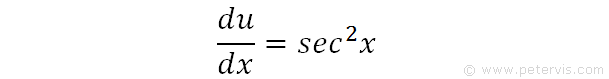
Then, du/dx = sec²x. This is a standard derivation found in formula books.

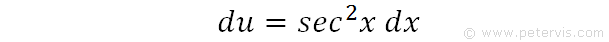
We rearrange it for du, so that the RHS is sec²x dx.

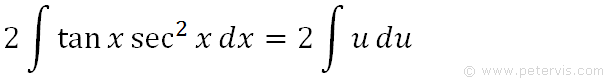
We can now replace sec²x dx with du, and also replace tanx with u, as shown on the RHS. This gives us a new integration expression that is much simpler in terms of u.

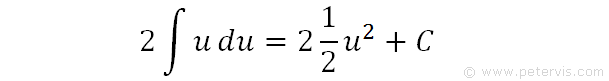
We integrate to get an answer in terms of u.

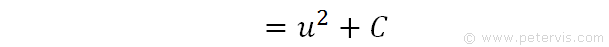
We now replace u with tanx.

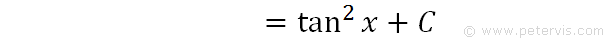
Hence, this is the answer. There are many trig identities involving tan²x, hence it is possible to change the form to something else should you require, however, for the most part it is best to leave it in this form.