Integrate cos^33x

To integrate cos^33x, also written as ∫cos³3x dx, cos cubed 3x, cos^3(3x), and (cos 3x)^3, we start by using a standard trig identity to change the form.

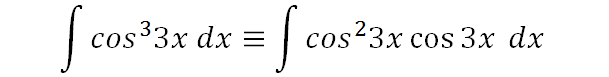
By factoring out one of the cos3x terms, we can bring the power down to 2.

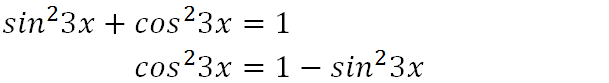
We recall the Pythagorean trig identity and rearrange it for cos3x squared term.

We substitute the rearranged trig identity into our integration problem. The substituted part is within the brackets.

We let u = sin3x.

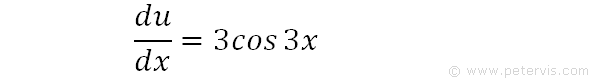
Then du/dx = 3cos3x. If you wish to know how to do this differentiation, then you can see it at the bottom of this page.

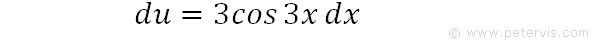
We rearrange the previous expression for du. As you can see, cos3x dx terms are the same as that in our integration problem. The only issue is with the constant multiplier 3, which prevents us from making a straight swap with du. In order to solve this issue we play a little trick as shown below.

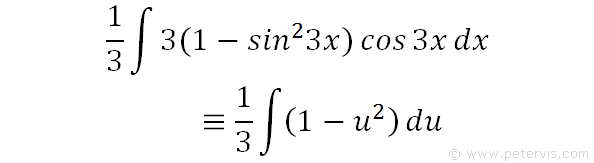
If we were to multiply ⅓ by 3, then the result would be 1 and we have not changed anything. However, the 3cos3x dx terms can now be removed, and we place du there instead. We can also replace the sin3x term within the brackets with u. As you can see, we now have a new expression that means the same thing, but is in terms of u and du.

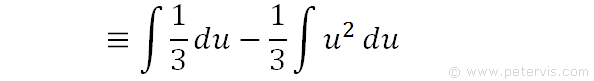
We multiply out the brackets, and integrate each term separately. The first term is a simple integration of a constant ⅓ which results in (⅓)u. The second term is also a simple integration of u squared.

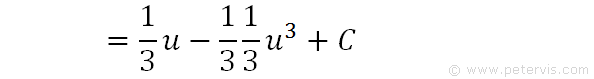
Hence, this is the intermediate result in terms of u. All that remains now is to replace u with sin3x to give the final answer.

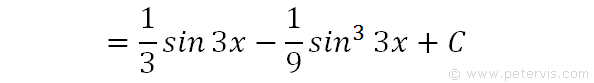
Hence, this is the final answer.

Differentiate sin3x