Integrate cosec^2x

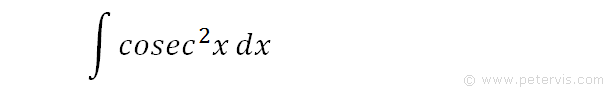
To integrate cosec^2x, also written as ∫cosec²x dx, cosec squared x, cosec^2(x), and (cosec x)^2, we start by using standard trig identities to simplify the integral.

We recall the standard trig identity for cosecx, and square both sides.

We divide the numerator and denominator by cos squared x.

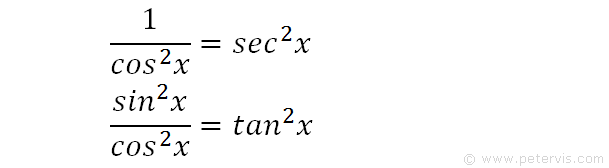
We recall the trig identities for sec squared x and tan squared x, and substitute them into the previous expression.

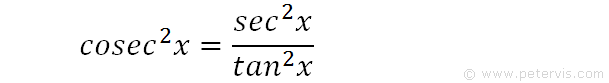
Hence, we get a new expression for cosec squared x.

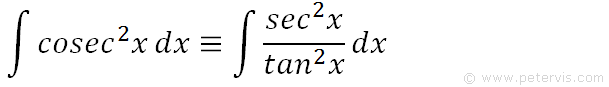
Hence, we get a new integration expression on the RHS, that means the same thing as the LHS. The purpose of making this change will become apparent in the next two steps.

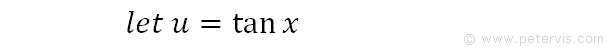
We let u = tanx.

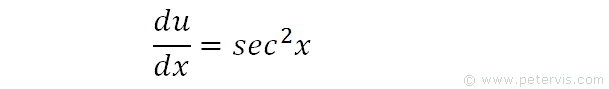
Then, du/dx = sec²x.

We rearrange it for du. As you can see, sec²x dx are the same terms in our integration problem, hence we can replace them with du.

We also replace tanx with u to give a new integration problem in terms of u and du.

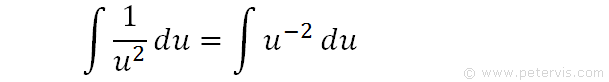
We change the reciprocal form so that it is easier to integrate.

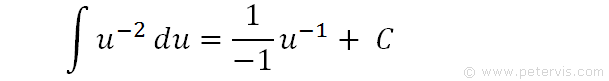
We then integrate w.r.t u to give an intermediate answer in terms of u.

We change it back to reciprocal form

We replace u with tanx.

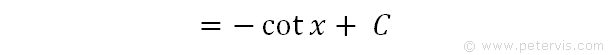
Hence, this is the final answer.