Integrate cos^22x
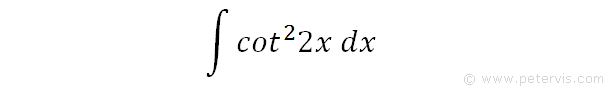
To integrate cot^22x, also written as ∫cot22x dx, cot squared 2x, (cot2x)^2, and cot^2(2x), we start by remembering that in formula booklets there is a standard proof showing the differential of cotx being -cosec2x. Therefore we need to use trig identities to change the form of this integral to something easier with -cosec2x. Hence we will drive this in that direction.

We recall a standard trig identity for cotx from our formula books. If we multiply all the angles by 2, then the equation remains balanced. We also square both sides thereby keeping the equation balanced, however, now the LHS looks like our integration problem.
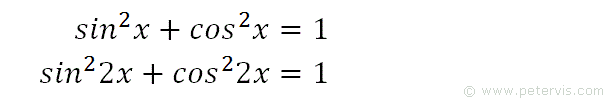
We recall this Pythagorean identity and adjust it as well by multiplying the angles throughout by 2, and we also square all the terms.
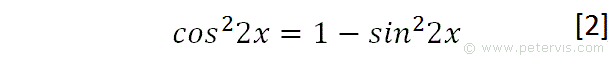
We then arrange the identity for cos22x.
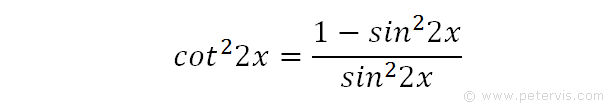
We then substitute identity [2] into identity [1] to give the above expression.
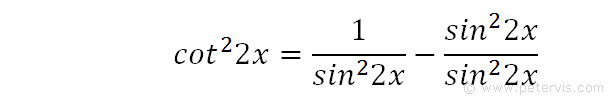
We expand out the denominator and notice that the sin22x terms cancel out.
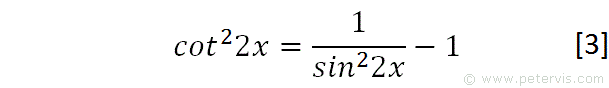
Hence we now have a new expression for cot22x as shown above.
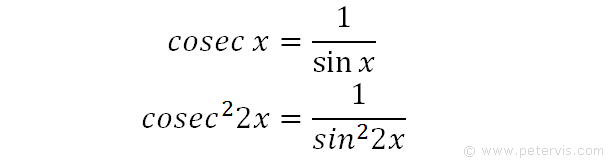
We now recall a trig identity involving cosecx. We adjust it by multiplying the angles by 2 and squaring both sides. Behold, for the RHS now looks just like the term in expression [3]. Therefore, we substitute it into [3] to give the expression shown below.
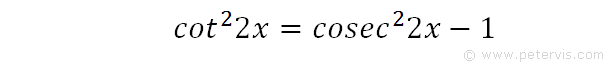
Now we have a new expression for cot22x in terms of cosec22x, which is exciting! This is what we have been aiming for all along and took all this time.
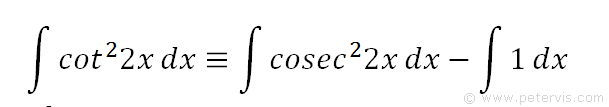
Therefore our original integration problem can be expressed in a new form which means the same thing, but easier to solve.

Back in the college days, you might recall a differential proof of cotx, or at least have seen it in one of the formula books. As you can see the differential of cotx is -cosec2x, which is almost like the first term of our integration problem. Mathematicians often call this the recognition asect, however where I come from , almost all of maths is about being able to recognise things. The problem here is that the angle is x and we need 2x.

What if we were to differentiate cot2x? Perhaps its derivative will have 2x for the angle and look more like the first term of our integration problem.

So, lets have a look and see what the derivative of y=cot2x looks like.

We let u=2x.

Hence du/dx=2.

We make the function y in terms of u.
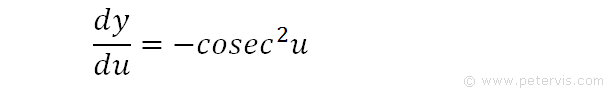
Hence, dy/du is -cosec2u. We know the differential of cotx from formula books as explained before.

This is usually used when differentiating a function of a function. As you can see the du terms cancel out.
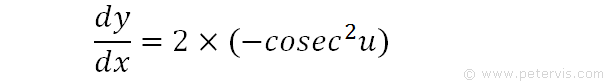
We substitute for du/dx and dy/du to give the above expression.
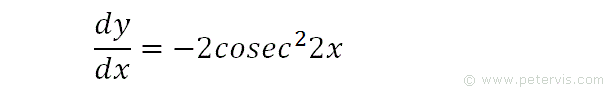
We then simplify it.
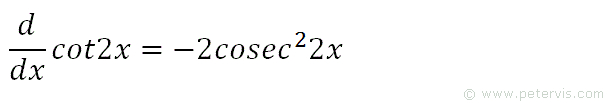
So to recap, the differential of cot2x = -2cosec22x.
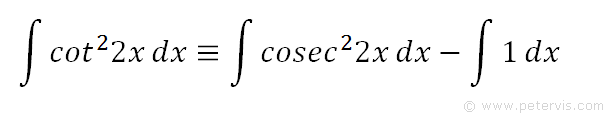
The first term on the RHS (cosec22x) looks very similar to the differential of cot2x, the only difference being -2 before it. However there is a little trick to get around this issue, as shown below.
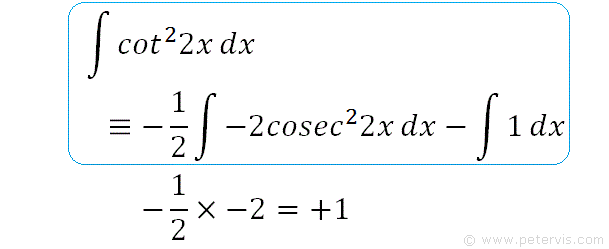
If we multiply -½ by -2 then we are not changing anything. Therefore we place a -½ outside the integral sign, and -2 before cosec22x. Therefore -½ × -2cosec22x = +cosec22x. Now the differential will fit!
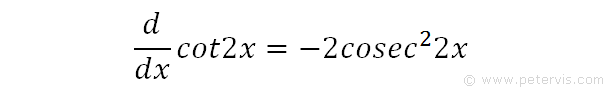
We recall the differential of cot2x that we found earlier. If we were to integrate the differential, then the result would be cot2x, which is common sense. However we need to show this mathematically.
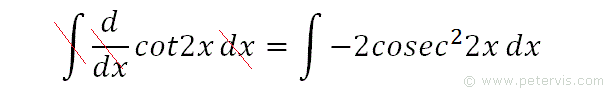
We integrate both sides, and therefore the operators on the LHS cancel out.
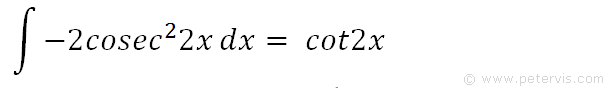
Therefore the integral of -2cosec22x = cot2x
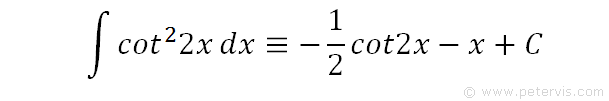
We can now substitute it into the first term on the RHS. We also remember the -½ behind the integral and reintroduce it. The lone x comes from integrating the constant 1, and C is the final integration constant.