Integrate cot^23x
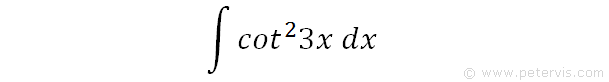
To integrate cot^23x, also written as ∫cot23x dx, cot squared 3x, (cot3x)^2, and cot^2(3x), we start by remembering a standard proof found in formula books where the differential of cotx is -cosec2x. If we can convert cot23x into a form that has cosec23x then we can use the recognition aspect because its differential will very likely be the solution. Therefore, that is the plan, and we drive our trig identities such as to achieve this.
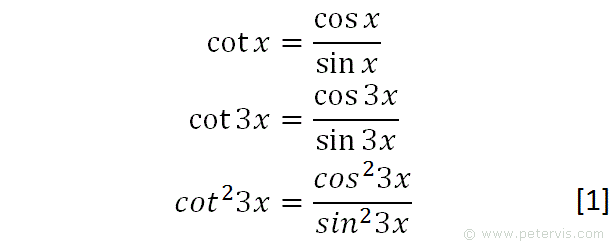
We recall the standard trig identity for cotx, and multiply the angles throughout by 3. We then square both sides to give expression [1].
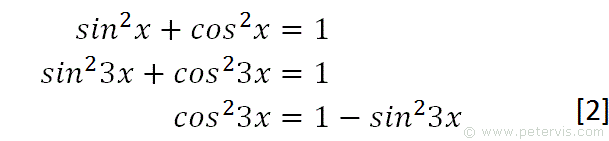
We recall the Pythagorean trig identity and multiply the angles throughout by 3. We then transpose it for cos23x to give expression [2].
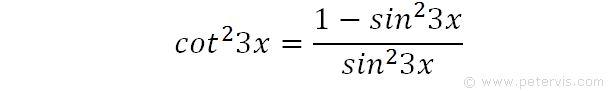
We then substitute expression [2] into expression [1] to give the above expression.
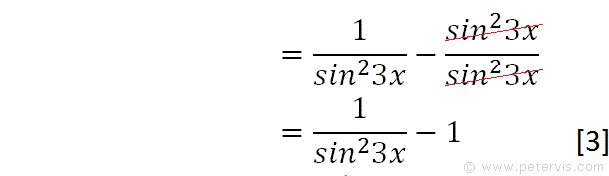
We then expand out the fraction and simplify because the sin23x terms cancel out.
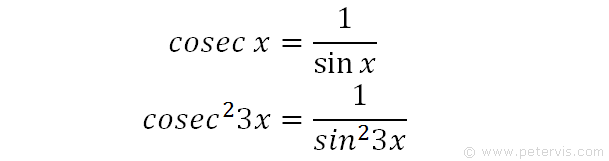
We recall another standard trig identity for cosecx, and multiply the angles throughout by 3, and square both sides. As you can see the RHS looks like the first term in expression [3]. We therefore substitute it into expression [3].
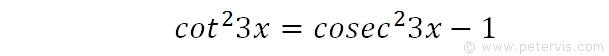
Hence we get this new expression for cot23x in terms of cosec23x.
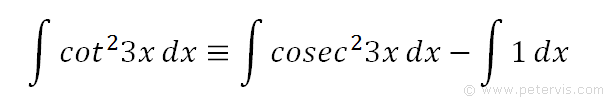
Hence we can now rewrite our original integration problem in another form that means the same thing but is simpler to solve. The first term (on the RHS) will need more thinking, but the second term is simple to integrate, and is x.
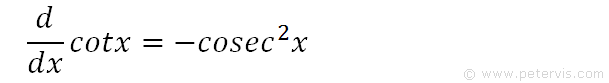
We recall this differential proof from formula booklets, and the result looks very much like the first term of our integration problem. The only difference being in the angle, where instead of x it should be 3x.

To get the angle correct, we consider the differential of cot3x. Perhaps it will have the correct angle...

We now focus our attention on y=cot3x and its differential.

Let u=3x

Then du/dx=3

We rewrite the function in terms of u by simple substitution.
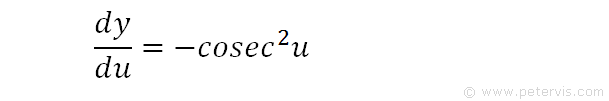
Then dy/du=-cosec2u

When we have function of a function something like this works well. As you can see the du terms cancel to give dy/dx.
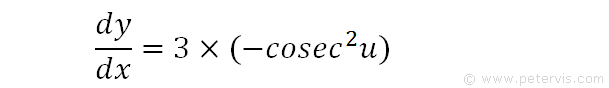
Hence we substitute the terms we previously found to give the above expression.
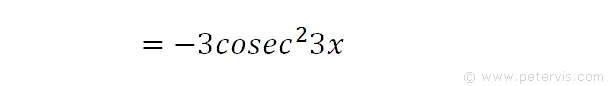
We then simplify and make it look neater.

Hence to recap, the differential of cot3x is -3cosec23x. As you can see, the RHS looks almost like the first term of our integration problem shown below. The only issue is the -3 multiplier. To solve this issue, we use a cunning little trick.
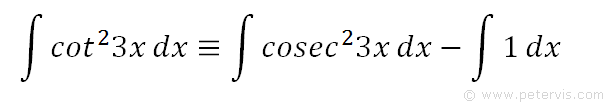
Recap of our original integration problem.
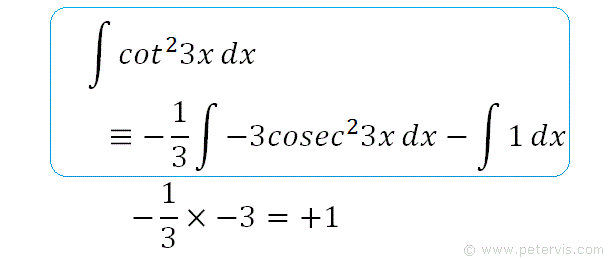
As you can see -⅓ × -3 = +1, therefore we are not changing anything, however now the first term of the integration problem looks exactly like the differential of cot3x.
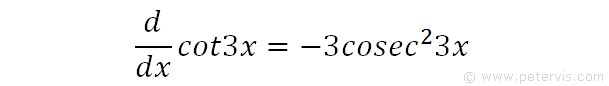
So now we have a solution for the first term, however we need to show mathematically, using the correct operators, that this is indeed the solution.
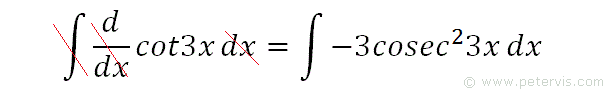
If we integrate both sides, then the operators on the LHS cancel.
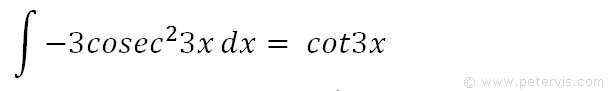
Hence the integral of -3cosec23x is cot3x.
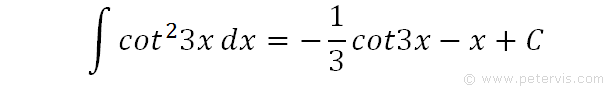
We now substitute the solution for the first term and also reintroduce the -⅓ constant that was outside of the integral sign. We integrate the constant 1 to give x, and C is the final integration constant.