Integrate sec^23x

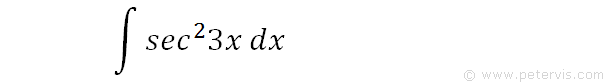
To integrate sec^23x, also written as ∫sec²3x dx, sec squared 3x, (sec3x)^2, and sec^2(3x), we start by using the u substitution.

Let u=3x.

Then du/dx=3

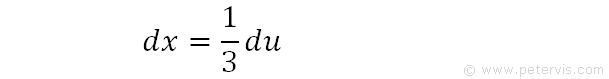
We rearrange for dx in terms of du.

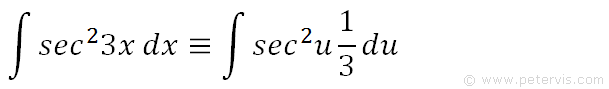
As you can see, we can rewrite the integration problem in terms of u by substituting out 3x and dx. It is much more simpler and means the same thing as the original integration problem.

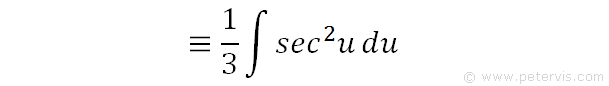
This is the same thing, except we have moved the constant 1/3 outside of the integral.

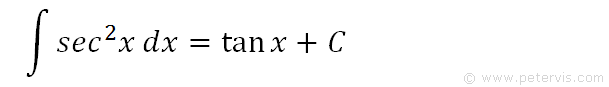
I have already shown how to integrate sec^2x in previous articles and, therefore; we take the proof from there as shown above. You should consult the other article as well to satisfy yourself.

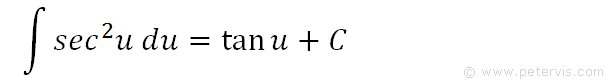
Therefore we rewrite it with u as it is in our case.

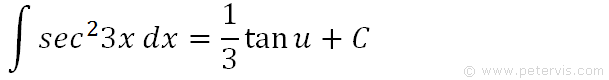
We substitute the solution back into our original integration reintroducing the constant 1/3 that was behind the integral.

We recall that u=3x, hence we substitute that in as well so that everything is in terms of x.

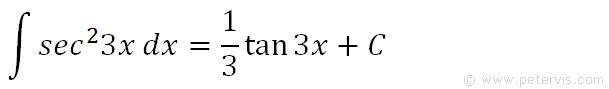
Hence here is the solution, where C is the integration constant.