Integrate sec^2x - Method 2

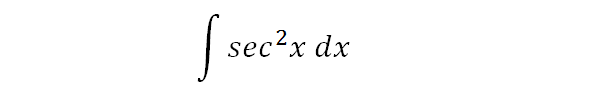
To integrate sec^2x, also written as ∫sec²x dx, sec squared x, and (sec x)^2, we start by using standard trig identities to simplify the integral. This solution uses the recognition aspecit of integration, where we might recognise a derived function. This type of skill often leads to simpler solutions.

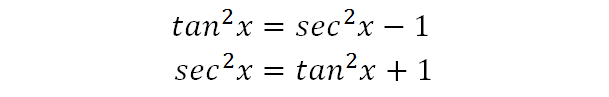
We start by using a standard trig function tan²x=sec²x-1, and rearranging it for sec²x.

we recall that tan²x=sin²x/cos²x, hence we substitute that into the previous expression to give the above.

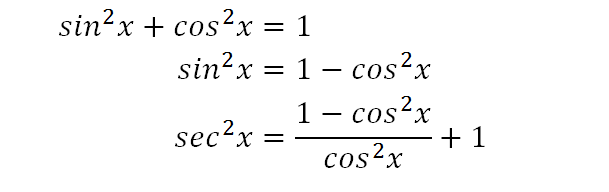
We recall the Pythagorean trig identity and rearrange it for sin²x, and then substitute that into our expression to give the above.

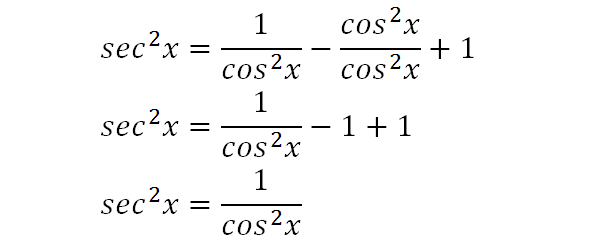
We then break up the fraction and simplify. The cos²x terms cancel to give 1, and the 1's cancel out as well to give a very simple expression for sec²x.

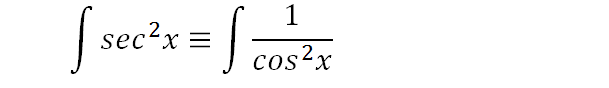
Hence, we now have a new integral in terms of cos²x that means the same thing and is simpler to solve.

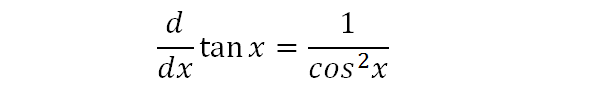
At this point, the recognition aspect should kick-in to remind you that the differential of tanx is exactly what we are integrating, therefore, we know that the answer to our problem is tanx. This is a standard rule also found in examination booklets, however we must prove it!

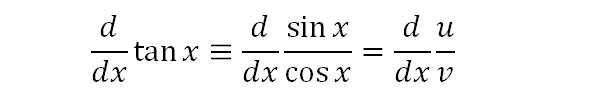
As you can see, the differential of tanx is the same as the differential of sinx/cosx. We can map that to the differential of a fraction u/v, and thereby use the differentiation of quotients rule.

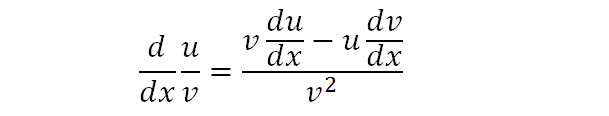
The differentiation of quotients rule is shown above.

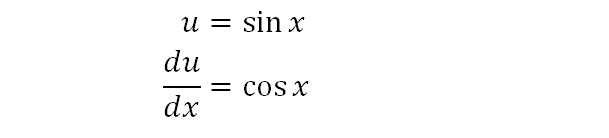
We map u to sinx and therefore its differential is cosx.

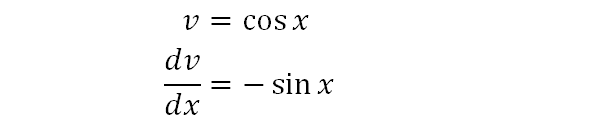
We map v to cosx, and therefore its differential is -sinx.

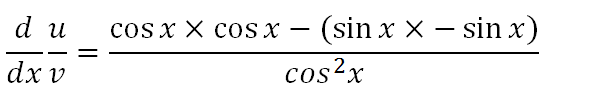
We now substitute everything we found in the previous steps into the quotients rule formula to give the above expression.

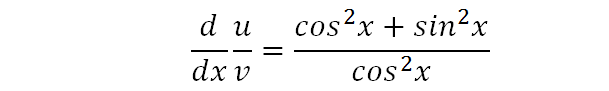
We now simplify to give the above expression.

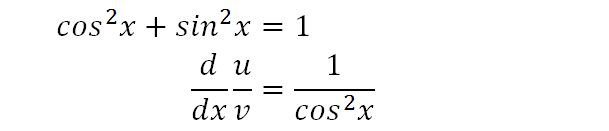
We use the Pythagorean identity to simplify further.

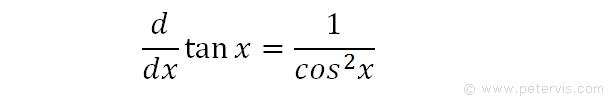
Finally, we prove that the differential of tanx is 1/cos²x. Therefore, if we were to integrate 1/cos²x, then the answer would be tanx + C where C is the integration constant.