Integrate secx

To integrate secx, also written as ∫secx dx, and sec x, we start with a commonly used trig manipulation so that we can change the form to one that allows the use of u substitution.

If we multiply and divide by (secx + tanx), then we have not changed anything, because they cancel out. However it helps to change the form to one suited for substitution.

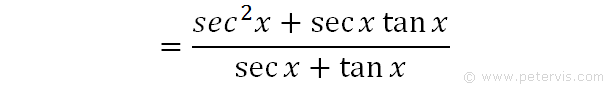
We multiply the terms in the numerator by secx to simplify.

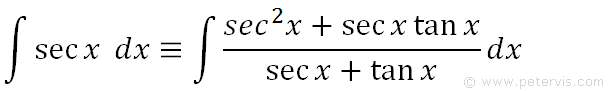
As you can see, our original integration problem is now in a new form that means the same thing but is simpler to solve.

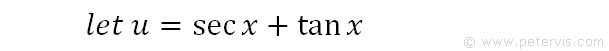
Let u=secx + tanx.

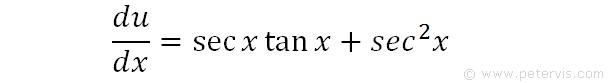
Then du/dx=secx tanx + sec²x. We differentiated each term separately, and the differentials of tanx and secx can be found from formula booklets. Notice that the differential (RHS) is exactly the same expression we have in the numerator of our integration problem. This was the reason for the trig manipulation.

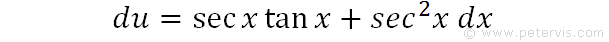
We rearrange our expression for du by moving dx on the other side.

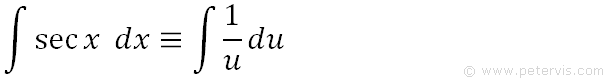
As you can see, now our original integration problem can be written in terms of u only and it means the same thing except it is much more simpler.

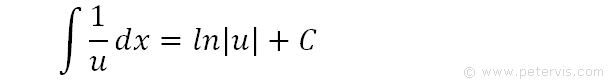
The integration of 1/x is a standard proof found in formula booklets. Hence the integral of 1/u is ln|u|.

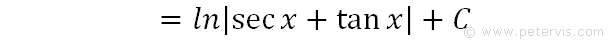
We replace u with secx + tanx, and C is the integration constant. Hence, the answer is ln|secx + tanx| + C