Integrate sin2x

To integrate sin2x, also written as ∫sin2x dx, and sin 2x, we usually use a u substitution to build a new integration in terms of u.

Let u=2x.

Then du/dx = 2

We rearrange to get an expression for dx in terms of u.

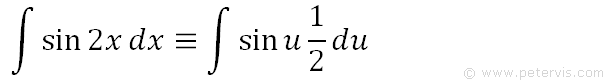
As you can see, we now have a new integration in terms of u, which means the same thing. We get this by replacing 2x with u, and replacing dx with ½ du.

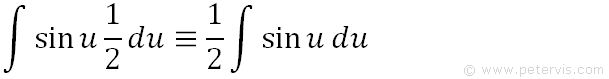
We move the ½ outside of the integral as it is simply a multiplier.

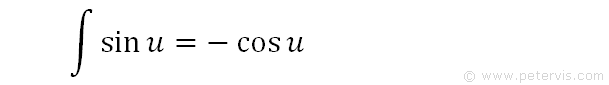
We now have a simple integration with sinu that we can solve easily.

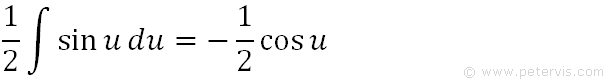
We remember the ½ outside the integral sign and reintroduce it here.

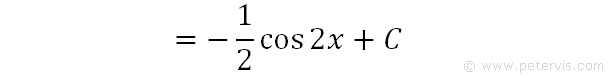
Hence, this is the final answer -½cos2x + C, where C is the integration constant.