Integrate sin^22x cos^22x
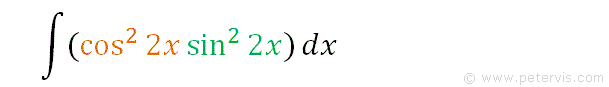
To integrate sin^22x cos^22x, also written as ∫cos22x sin22x dx, sin squared 2x cos squared 2x, sin^2(2x) cos^2(2x), and (sin 2x)^2 (cos 2x)^2, we start by using standard trig identities to change the form.

We recall the Pythagorean trig identity and rearrange it for cos squared x to make [1]. We recall the double angle trig identity and rearrange it for sin squared x to make [2]. We then substitute [2] into [1] and simplify to make identity [3].
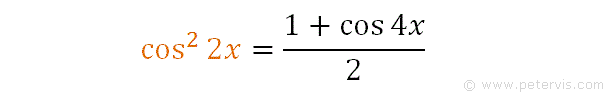
As you can see identity 3 is almost like the cos squared part of our integration problem except it has 2x for the angle. If we multiply the angles on both sides by 2, then as you can see, we get the cos squared 2x term, as shown above.

We repeat the steps using the Pythagorean trig identity and the double angle identity, except we get the sin squared x term as shown at [4].
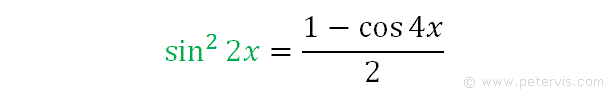
We multiply the angles on both sides by 2 to get the above trig identity.
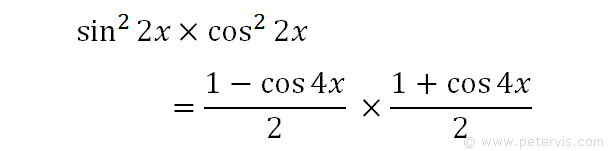
As you can see, we now have an equivalent trig identity that we could integrate, however it still requires simplification.
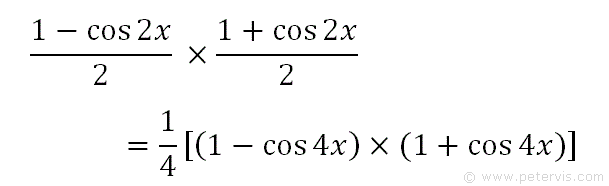
With the denominators multiplied and out of the way, we can focus on multiplying the numerators.
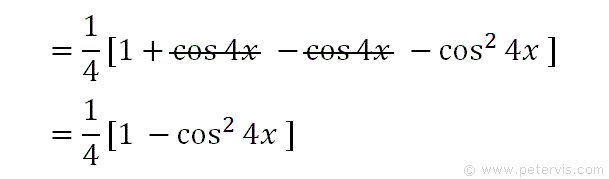
As you can see, the cos4x terms cancel out. And we get a simpler expression, however it still has a cos squared term that makes integration prohibitive.
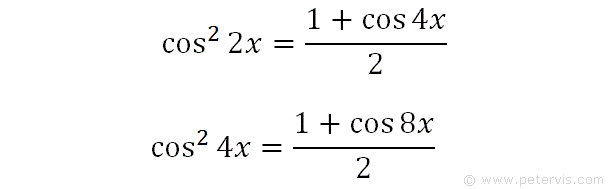
We recall the trig identity for cos squared 2x that we previously made, and multiply the angles by 2 on both sides again, to give the identity above.
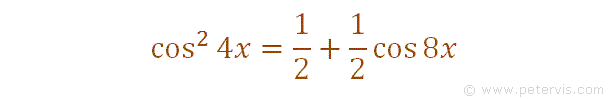
We simplify it further by separating the terms in the numerator.
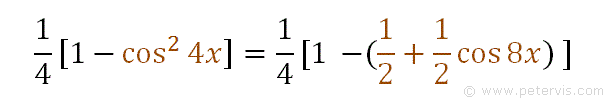
We can now replace the cos squared 4x term in our previous expression.
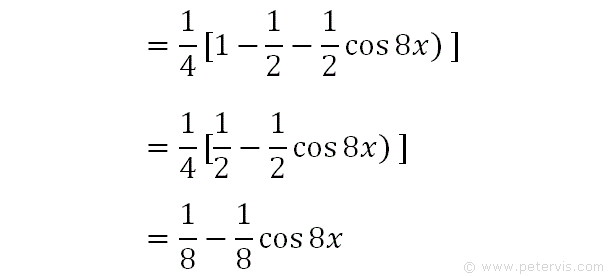
We simplify the expression further to give the final identity.
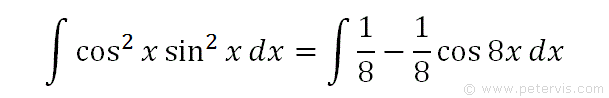
Hence, our original integration problem can be writtin in a new form as shown above. It involved trig manipulation steps as shown above.

We can integrate each term separately as shown in the RHS. The first term is a constant and simple to integrate, however we need to focus on the second term. This part is shown below in red.
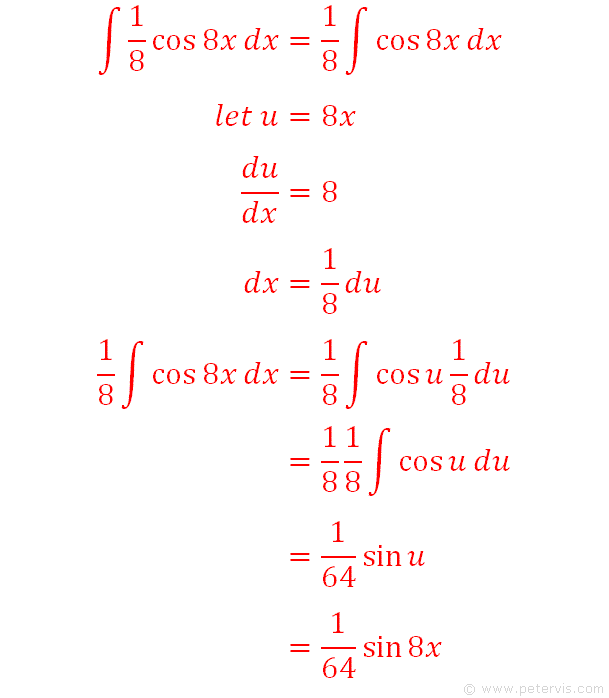
We integrate the second term and get the answer as shown above in red. All that remains now is to substitute this part of the solution into our integration problem.
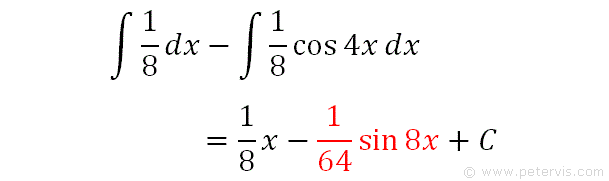
Hence, this is the final answer, where C is the integration constant.