Integrate sin^23x

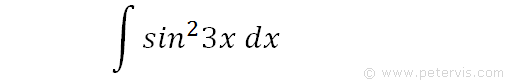
To integrate sin^23x, also written as ∫sin²3x dx, sin squared 3x, (sin3x)^2, and sin^2(3x), we start by using a u substitution.

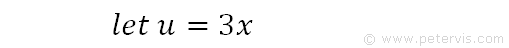
Let u=3x.

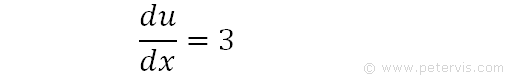
Then du/dx=3.

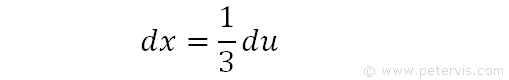
We then rearrange the previous expression for dx.

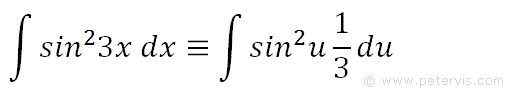
We then rewrite the integration problem in terms of u by substituting out the dx, and 3x. On the RHS we have a simpler integration in terms of u, which means the same thing.

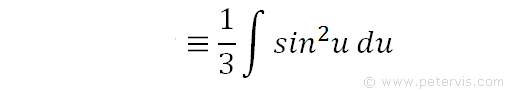
We simplify by moving the constant 1/3 outside of the integral. As you can see, we now need to integrate sin²u.

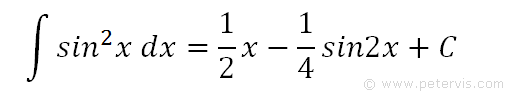
As it just so happens, I have already shown how to integrate sin^2x, and therefore we can use the above result that we had previously obtained.

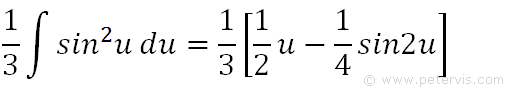
Therefore in our case it is in terms of u as shown on the RHS.

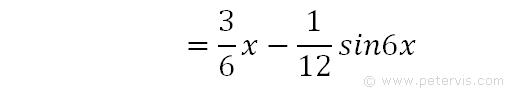
We then simplify and substitute back the 2x for u.

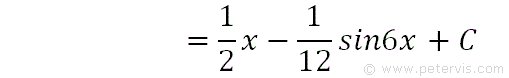
We then simplify further, and this is the answer.