Integrate sin^32x

To integrate sin^32x, also written as ∫sin³2x dx, sin cubed 2x, sin^3(2x), and (sin 2x)^3, we start by using standard trig identities to simplify the integral.

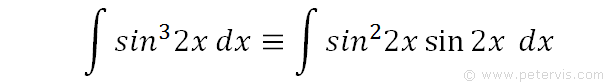
We factor out one of the powers, and therefore the new expression is the same integration.

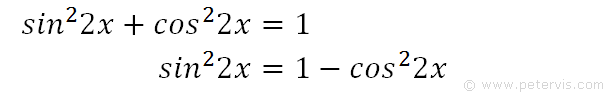
We recall the Pythagorean trig identity and multiply its angles by 2. We then rearrange it for sin^2(2x) so that we can substitute it into our integration problem.

With the substitution, we now get a new expression that means the same thing.

Let u = cos2x

Then du/dx = -2sin2x. You can see how to do this differentiation in the aside section at the bottom of the page.

We rearrange the expression for du. As you can see, it is almost identical to the part outside the brackets in our integration problem, except that this has a -2, otherwise we could substitute du for it. To solve this issue we play a small mathematical trick.

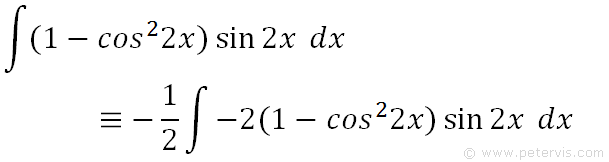
If we were to multiply -½ by -2 then the result would be +1 and we have not changed anything. However -2sin2x dx can now be replaced by du.

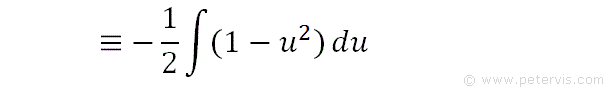
We also replace cos2x by u, so that the integration is in terms of u. The new expression means the same thing, except it is easier to solve.

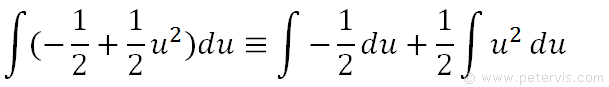
On the LHS we multiply out the -½. On the RHS we integrate each term separately, which means the same thing.

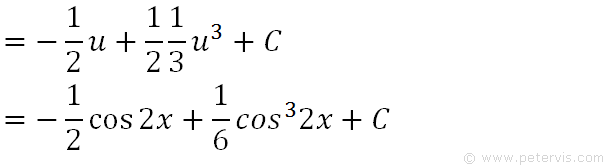
We finally integrate and replace u by cos2x. Hence this is the solution.

Differentiate cos2x