Integrate tan^22x

To integrate tan^22x, also written as ∫tan²2x dx, tan squared 2x, (tan2x)^2, and tan^2(2x), we start by utilising standard trig identities to change the form of the integral. Our goal is to have sec²2x in the new form because there is a standard integration solution for that in formula booklets that we can use.

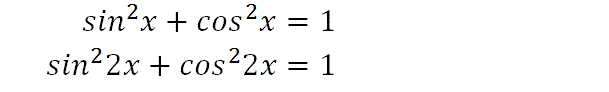
We recall the Pythagorean trig identity, and multiply the angles by 2 throughout to keep the equation in balance.

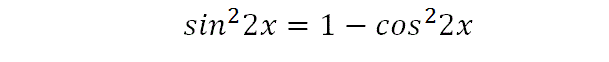
We rearrange the trig identity for sin²2x.

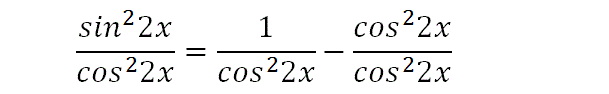
We divide throughout by cos²2x.

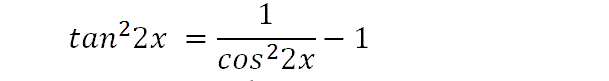
The LHS becomes tan²2x, which is our integration problem, and can be expressed in a different form shown on the RHS. However, we still need to make some changes to the first term on the RHS.

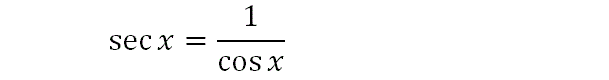
We recall a standard trig identity with secx. This is usually found in formula books.

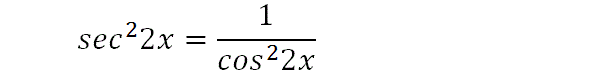
We square both sides, which makes the RHS look like the term we had in previous steps.

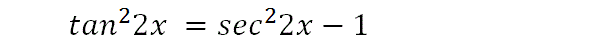
Hence we can now substitute that so that our expression has sec²2x. The reason why we went through all this was to bring this term into our expression. It will all become clear in the following two steps.

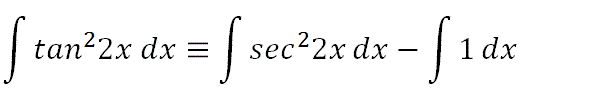
We can now express our original integration problem in another form that means the same thing and is simpler to do.

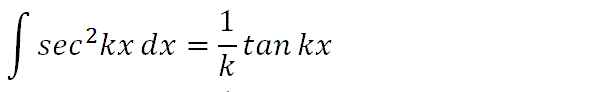
We recall a standard integration usually found in formula booklet for sec²kx. As you can see, there is a straight solution for this integration.

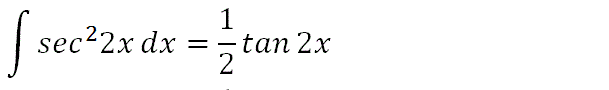
Hence, for our problem the integration solution for this part is shown above.

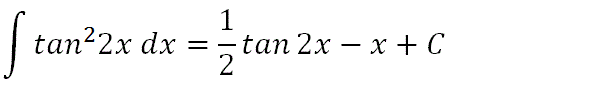
Hence, this is the final solution, where C is the integration constant.