Integrate tan^23x

To integrate tan^23x, also written as ∫tan²3x dx, tan squared 3x, (tan3x)^2, and tan^2(3x), we start by utilising trig identities to change the form.

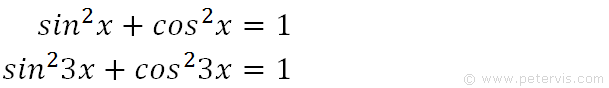
We recall the Pythagorean trig identity and adjust it by multiplying the angles by 3.

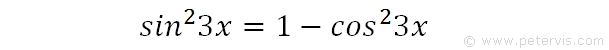
We then rearrange it for sin²3x.

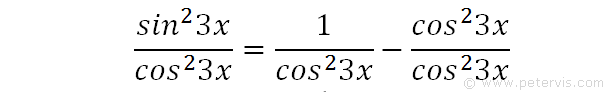
We now divide throughout by cos²3x.

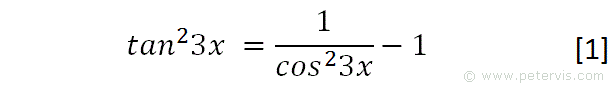
As you can see, the LHS looks like our integration problem.

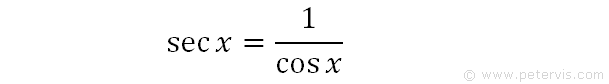
We recall this simple trig identity for secx.

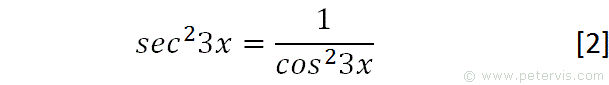
We adjust the identity by multiplying the angles by 3, and squaring both sides.

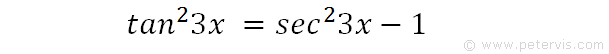
We substitute expression [2] into expression [1] to get a new expression with sec²3x.

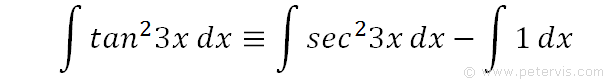
Hence, we can rewrite our original integration problem, as shown above. The RHS shows a different form that means the same thing.

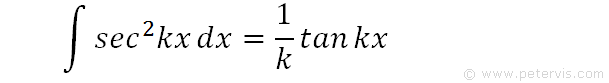
We recall a standard proof from formula books. Back in my days, I did "A" levels and the formula booklet had one of these.

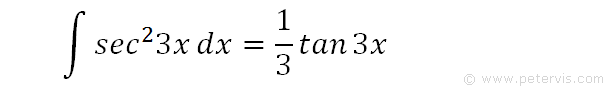
Therefore, in our case, this is the result for the first term on the RHS.

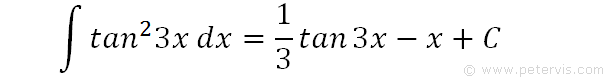
Hence, this is the final answer, and C is the integration constant.