Integrate tanx

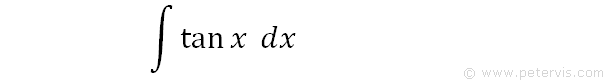
To integrate tanx, also written as ∫tanx dx, we start with a trig identity to change the form.

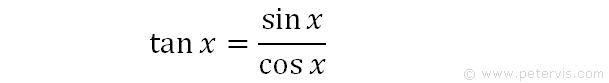
We use this well-known trig identity to change the form.

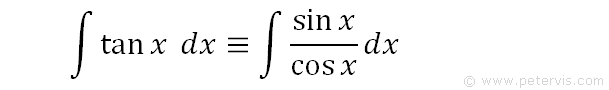
Hence, our integration problem can be rewritten in a different form yet it means the same thing.

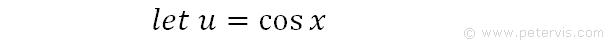
We recognise that when we differentiate the denominator the result looks like the numerator and therefore we let u=cosx.

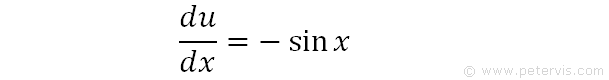
Therefore du/dx=-sinx

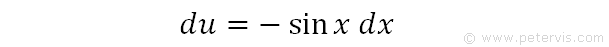
We rearrange the expression to give du. As you can see, it looks like the numerator except for the negative sign. If it was not for the negative sign, we could substitute sinx dx with du. To solve this issue, we play a little trick.

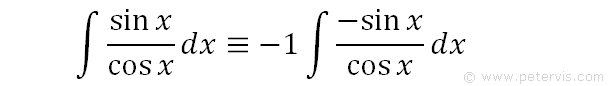
If we multiply -sinx with -1 then the negatives cancel and we get +sinx, therefore we have not changed anything. However now, the numerator is exactly right for substitution.

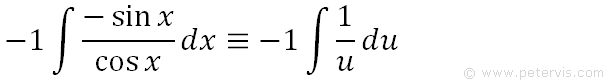
We therefore replace -sinx dx with du, and cos x with u. As you can see, now the integration problem is in terms of u and simpler to solve.

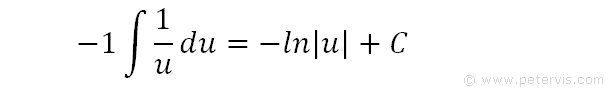
We look up integral in our formula book for 1/u and find that it is -ln|u| + C. We also reintroduce the -1 behind the integral sign.

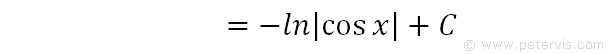
In this step, we replace u with cosx.

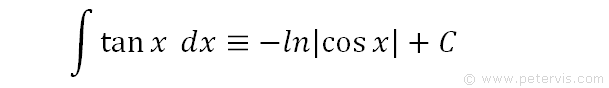
Therefore, ∫tanx dx = -ln|cosx| + C.