Integrate xe^x^2

∫ xe^x^2 dx: Integrating this is extremely simple and ideal for beginners. Using the u substitution method is the best way to solve it.

All that I have done here is move x closer to dx and it is still the same expression. The purpose of moving it is to group x dx together as this is the part I will be substituting out. Hence, it is just for clarity for beginners so they can follow better this way.

The substitution is u = x^2. For beginners the main question seems to be, "How do you determine when to use the substitution method?" A rough rule is that if the derivative of u looks anything like the outside part x dx then substitution will have a good chance of working.

The derivative of u is 2x which is a good indicator that substitution will work as there is a x dx in the problem.

The goal here is to get an expression where x dx is on one side and all the unwanted terms on the other side, hence it is just a simple matter of transposition.

Here is an expression for x dx.

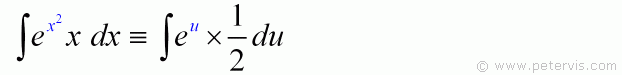
∫ e^x^2 x dx ≡ ∫ e^u ½ du: All that I am doing here is replacing x^2 with u, and also replacing x dx with the expression found earlier.

½∫ e^u du: This is just a bit of tidying up with ½ behind the integral. As you can see all you have to do now is to integrate e^u with respect to du which is a simple and straightforward integration.

At this stage we can now substitute u back in.

Finally, this is the answer.