Integration by Parts Derivation

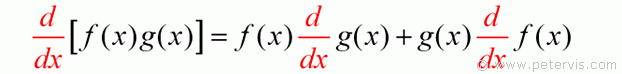
Deriving the integration by parts standard formula is very simple, and if you had a suspicion that it was similar to the product rule used in differentiation, then you would have been correct because this is the rule you could use to derive it.

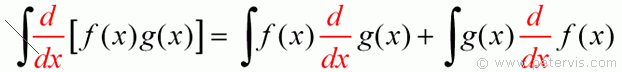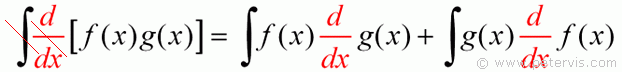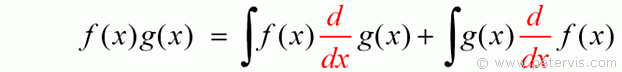
As you can see, we start out by integrating all the terms throughout thereby keeping the equation in balance. In mathematics, things always start looking incredibly complex just before they end up being ludicrously simple.

As you can see on the LHS, when you integrate and differentiate the operator functions cancel each other out. I do not know what it is called though.

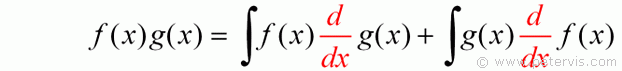
As you can see on the LHS, we end up with f(x) × g(x). Nice as it may seem, that part was not wanted! That was just a little bit of collateral cancellation that happened to be there and was completely unplanned. The part we are interested in is the following.

f(x) d/dx g(x)

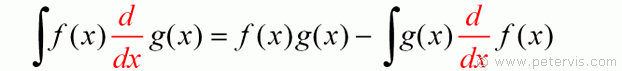
Then with a little bit of reorganisation moving the terms from one side to the other we have this familiar equation. The LHS is the bit that maps to your particular equation that you might be working on. As you can see the LHS might appear strange to you at first as it is not a straightforward f(x) × g(x) but instead f(x) and d/dx g(x). The d/dx g(x) confuses people but the function is already a derivative. Therefore, to get g(x) you simply integrate that part, and it will all become clear when you follow a couple of examples.

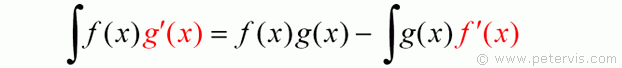
Here I am using the prime mark notation instead of d/dx to make it look simpler.

Some people prefer to use the integration by parts formula in the u and v form. To do that you simply substitute f(x) = u.

Substitute g(x) = v.

Then the derivative of f(x) is du/dx.

Finally, the derivative of g(x) is dv/dx.

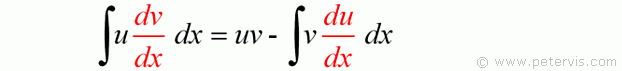
Then simply substitute everything into the previous formula to give this. You can satisfy yourself that this is indeed the same formula but with u and v instead. Many exam boards use this version of the formula instead; therefore, it is worth learning how to use it.

The LHS of the formula maps to your particular problem at hand. If you are trying to integrate a product of two functions then one part becomes u and the other part becomes dv/dx. The dv/dx simply means it is the derivative, so all you have to do is to integrate that part to give you v, which you substitute on the RHS of the equation. The rest of course is straightforward and simple.