Integration by Parts Exponential

∫ e ^ x dx: Integrating and differentiating an exponent is very easy and therefore this is a really nice and simple one that you can play around with for a few minutes for experimentation just to see what would happen.

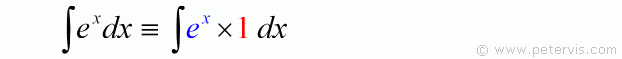
∫ e ^ x dx ≡ ∫ e ^ x × 1 dx: In order so that we can use the integration by parts formula we can multiply it by 1. It is the same expression and nothing has changed but it gives us a way to use the parts formula.

Choosing u=e^x, we can find its derivative easily which is e^x.

If dv/dx=1, then v=x, which is found by integrating 1 obviously.

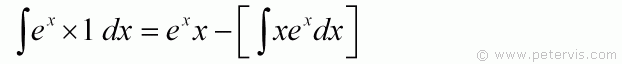
Substituting the values of u, v, and du/dx gives us the expression shown above. However, as you can see the RHS now has ∫ xe ^ x dx which is even more complicated than e^x. Therefore, it appears that with substitutions this way round, the final expression is more complicated; however, it is not impossible to do.

∫ xe ^ x dx = (xe ^ x) – (e ^ x) : Luckily, this proof was done earlier in the mathematics section so just refer to that example to find out how it is done. Nevertheless, since we know this, we can substitute this in to see what happens.

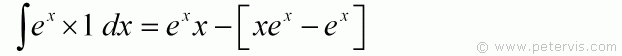
All I am now doing is substituting the previously found result into the brackets.

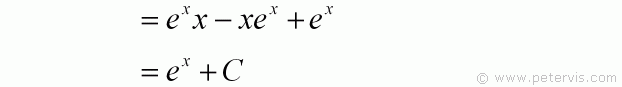
As you can see xe^x cancels out and we are left with e^x.

Substitution reversed

If we choose u = 1 this time, just to see what would happen this way round.

This time we choose dv/dx to be e^x, and therefore v=e^x as well.

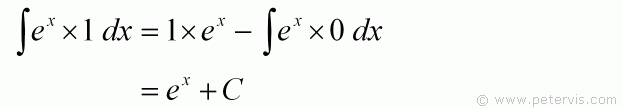
Substituting u, v, and du/dx into the integration by parts formula gives us this expression. The integral on the RHS cancels out when multiplied by zero and therefore this is a much better option to choose.