Boolean Algebra Example 2 Questions and Answers
In this Boolean example, you have a logic diagram consisting of gates, and your job is to find a Boolean expression that describes it. Once you have that, you should simplify it to minimize the number of gates it uses.
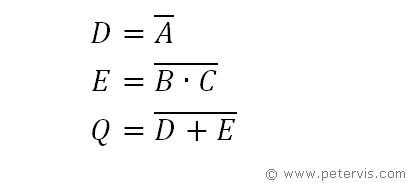
We start by writing the expressions for individual gates and their intermediate terms.
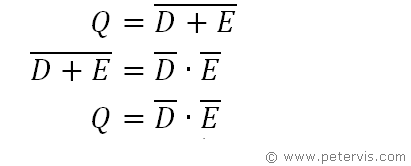
As you can see, there is that familiar term that requires De Morgan’s theorem, which we substitute into our equation.
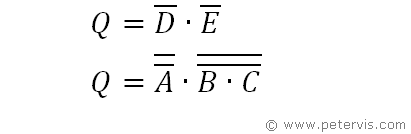
We now substitute for the D and E terms using expressions figured out previously. At this stage, we also get these double bars over our terms, which is like double negation. If you NOT something twice, then it negates itself.
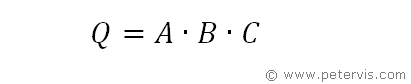
Finally, the answer is a three input AND gate, which does the same job.
Truth Table
| A | B | C | D | E | Q |
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 |
As you can see from the truth table, A AND B AND C gives the result in the Q column.
This Article Continues...
Boolean AlgebraDe Morgan's Theorem
XOR Gate
EXOR Gate
XNOR Gate
Example 1 Questions and Answers
Example 2 Questions and Answers
