Quadratic Equation Area Problems

Here is a floor plan of a building with the following dimensions. It is a six-sided shape where all the corners are right angles. All the measurements are in metres.

Question

If the total area of the building, shaded in yellow, is 24 m² show the following formula.

4x²+4x-24=0

Answer

Start by writing this expression shown above. The areas of the two rectangles add up to 24 obviously.

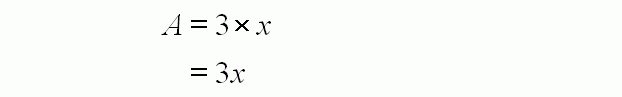
The area of rectangle A is its length multiplied by its width, or 3 × x.

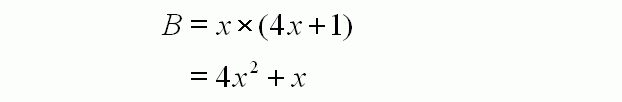
The area of rectangle B is also its length multiplied by its width. The length is (4x+1), and the width is x, making it (4x+1) × x. You then simply multiply each term in the brackets by x as shown above.

Since we know the expressions for A and B, we can plug them into the formula A + B = 24 as shown above.

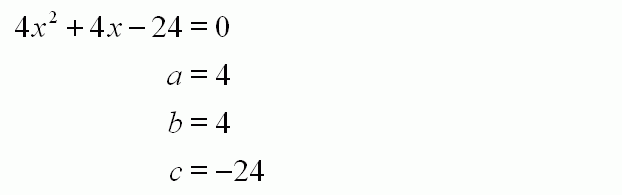
In this step, we bring the 24 to the LHS. We are algebraically subtracting 24 on both sides, so the RHS becomes zero. As you can see, we now have a quadratic equation, which is the answer to the first part of the question.

Question 2

In exam conditions, you may have to solve this equation, in which case you might have to use the general formula for solving quadratic equations.

Answer

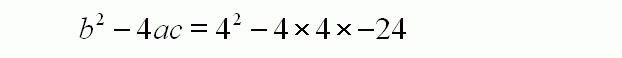
You always start by calculating the discriminant part. This is the bit under the square root sign of the general formula. In this case, it is a positive number 400. Therefore, it will have real roots, as opposed to imaginary roots had the number been negative.

This is the value of the discriminant part.

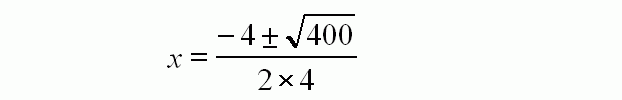
Just plug the coefficients into the general formula, together with the value for the discriminant, which you found earlier.

Finally, here are the two solutions for x. The answer is therefore 2 metres. We disregard the negative number because you cannot have a negative measurement in real life. You can also now also factorise to get (x - 2)(x + 3) which might be another question in an exam situation.