Quadratic Equation Area of Rectangle

In this example question, there are two rectangles, and you simply have to subtract the area of the smaller rectangle from the area of the larger rectangle to get the answer. The final expression is of course a quadratic equation that you can solve using the standard formula. I have designed the question so that the numbers can be easily calculated without a calculator.

Question 1

The diagram above shows a large rectangular piece of card of length 2x+3 and width x. A small rectangle is missing from one corner. The small rectangle has a length x and width 2 cm. The remaining shaded area is 21 cm².

Show that 2x²+x-21=0, and calculate the length of the smaller rectangle.

Answer

Cutout area problems are very simple to solve. If the area of the large rectangle is A, and the area of the small rectangle is B, then we can write the expression above. If you subtract the area of the small rectangle from the area of the large one the resulting area shaded in yellow equates to 21.

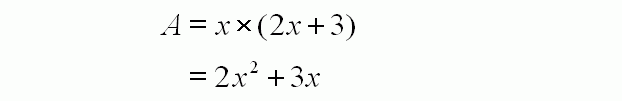
The area of the large rectangle A is (2x+3) × x, which is the multiplication of the length of its sides.

The area of the small rectangle B is 2 × x, which is the multiplication of the length of its sides.

We simply plug the expressions of the individual areas of A and B into the expression A - B = 21.

Subtract both sides by 21 to bring it over to the LHS. As you can see, we have a quadratic equation, which is the answer to the first part of the question.

To find the length of the smaller rectangle, you simply have to solve the quadratic equation, using the standard formula. The first step is to identify the coefficients a, b, and c as shown above.

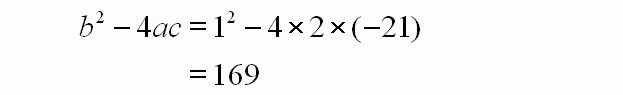
In the second step, you calculate the discriminant, which is the bit under the square root sign of the standard formula. As you can see, it is a positive number, which means that the roots will be real.

In the third step, you plug the rest of the coefficients including the discriminant into the formula to find the solutions for x.

They condense into these two terms.

Finally, these are the solutions. Therefore, 3 cm is the length of the smaller rectangle. We disregard the negative solution, as you cannot measure a negative amount in real life.