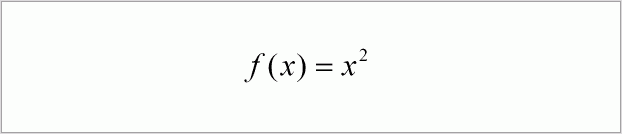Differentiation from First Principles

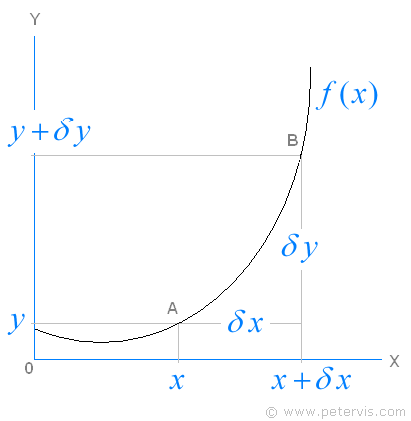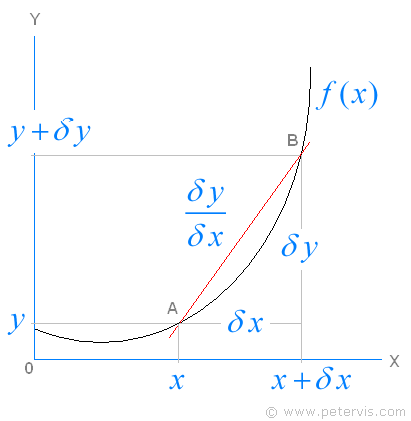
Here is a simple explanation showing how to differentiate x², also known as y=x^2 by first principles. It is one of those simple bits of algebra and logic that I seem to remember from memory. Mr Parsons first taught this to me at Carshalton College all the way back in the late 1980s.

Differentiation is about measuring the rate of change and usually one draws a gradient on a curve to calculate it. If you wanted to know the gradient at a point (x, y), then you would draw a line touching the curve at point (x, y), but in this case we draw a line between two points A, B, on the curve. Obviously, this will not give us the exact gradient because the line is cutting the curve and not touching it. Therefore there will be an error introduced, however as the points A and B get closer the amount by which the line is cutting the curve reduces and therefore the error reduces also.

As you can see, as the points A and B get closer, δx reduces and so does the error. In addition, an algebraic magic trick will later diminish the error entirely.

y=x², or y=x^2

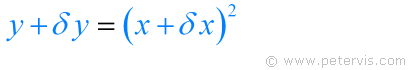
Replacing x with (x + δx), and y with (y + δy) in the function y = x² gives the expression shown above. You can see where these terms fit on the graph above.

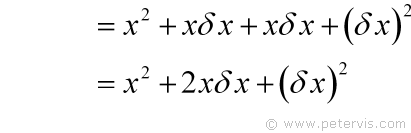
On the RHS, you can now multiply out the binomial expression. Before it was nice, clean, and minimalistic, and now it is full of terms that will need sorting out. There are some parts that we will keep, some that we will remove by transposition, and others we can make disappear using a magic trick.

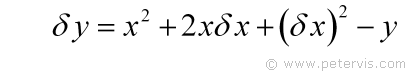
At this stage, we can move the y to the RHS. What I am aiming to do is to have δx / δy on the LHS, and since I already have δy there, I only need to move δx.

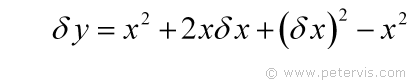
On the RHS, I can replace y with x² by substitution, and now I have +x² and -x², which cancel each other out.

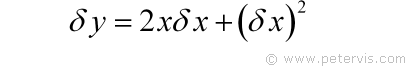
Now we have something simpler. If I divide throughout by δx then on the LHS I will have δy / δx. Therefore, this seems like a good move.

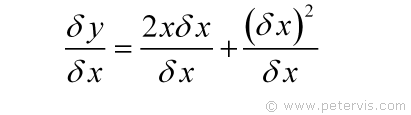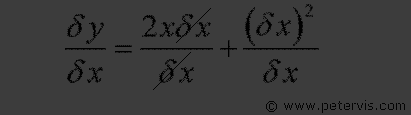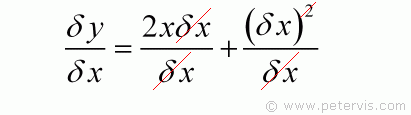
On the RHS, you can see that δx from the top and bottom cancels out.

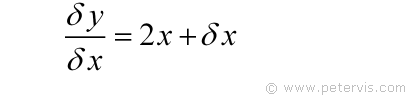
Now we have something simpler and it is almost there as dy/dx = 2x, but the only problem is that there is a small amount of error given by δx. However, we know that as we bring points A and B closer the error diminishes.

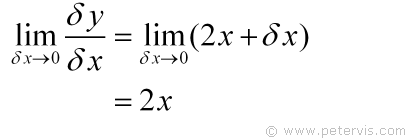
At this stage we apply a little algebraic magic trick is to say that as δx approaches zero, the error also approaches zero, and therefore the implicit derivative is 2x.

The last time I was playing with something remotely similar was when reading a paper on rolling tachyons in string theory.

This Article Continues...